近日,信息科學(xué)與工程學(xué)院講師徐敬可在《IEEE TRANSACTIONS ON COMMUNICATIONS》在線發(fā)表了題為“Folded Polynomial Codes for Coded Distributed AA^T-Type Matrix Multiplication”的研究論文。徐敬可老師為該論文的第一作者。
得益于分布式計(jì)算平臺(tái)和分布式計(jì)算框架的優(yōu)良性能,以大規(guī)模矩陣乘積為核心的機(jī)器學(xué)習(xí)算法和大數(shù)據(jù)分析技術(shù)得到了快速發(fā)展。然而,由于網(wǎng)絡(luò)延遲、資源共享、系統(tǒng)維護(hù)和功率限制等因素,分布式計(jì)算系統(tǒng)的工作節(jié)點(diǎn)會(huì)出現(xiàn)暫時(shí)失效等未能完成計(jì)算任務(wù)的問題,我們稱之為稱為節(jié)點(diǎn)掉隊(duì)問題。
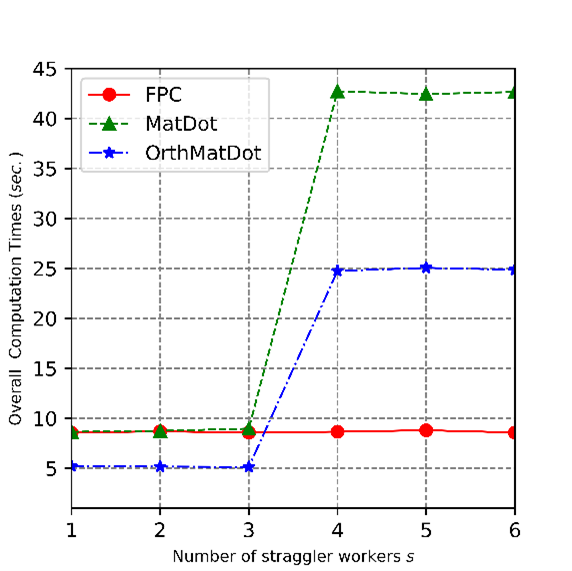
為了緩解節(jié)點(diǎn)掉隊(duì)的影響,針對(duì)矩陣與其轉(zhuǎn)置矩陣乘法,本研究利用折疊多項(xiàng)式設(shè)計(jì)了一類的新穎高效的分布式編碼算法。本文的關(guān)鍵技術(shù)是利用對(duì)稱性,將解碼問題轉(zhuǎn)化為折疊多項(xiàng)式的重構(gòu)問題,進(jìn)而利用無(wú)向圖的連通性確定了折疊多項(xiàng)式碼的恢復(fù)閾值。與現(xiàn)有算法相比,在保持原有節(jié)點(diǎn)計(jì)算復(fù)雜度的前提下,折疊多項(xiàng)式碼可以忍受更多的掉隊(duì)節(jié)點(diǎn),有更小的通信代價(jià)、更低的譯碼復(fù)雜度等優(yōu)勢(shì)。在相同掉隊(duì)節(jié)點(diǎn)的情形下,由于具有抵抗更多掉隊(duì)節(jié)點(diǎn)的優(yōu)良性能,折疊多項(xiàng)式碼可以應(yīng)用于更經(jīng)濟(jì)的分布式計(jì)算平臺(tái)。因此,該研究具有更廣泛的應(yīng)用價(jià)值。
該研究得到了國(guó)家自然基金項(xiàng)目、國(guó)家重點(diǎn)研發(fā)計(jì)劃項(xiàng)目、山東省自然科學(xué)基金項(xiàng)目、山東省“青創(chuàng)團(tuán)隊(duì)計(jì)劃”項(xiàng)目、廣東省基礎(chǔ)與應(yīng)用基礎(chǔ)研究基金項(xiàng)目的資助。
原文鏈接:DOI: 10.1109/TCOMM.2023.3286420
編 輯:萬(wàn) 千
審 核:賈 波









